Input Power

Typically, on a loudspeaker driver specification, an input power rating is specified. Most often, there are 2 numbers reported –average power and peak power specs. Although the essence is the same, an audio engineer sourcing a driver for a given application: telecom, fire and safety, telematics, among others, has a slightly different perspective than your average home stereo buyer. We’ll focus on our typical customer, here.

The average power, often referred to as RMS power, is the electrical power that can be continually used by a driver without damaging the speaker – overheating of the voice coil, deformation of the suspension (spider, surround). Due to it’s slowly manifesting nature, heat is the main driver of this rating. This comes in the form of I²R losses in the voice coil (P=I²R is one of the equations used to determine power).

When considering this rating, a rule of thumb is to consider the peak-to-peak supply voltage available in the product using the loudspeaker driver to serve as the sound source. Another power equation is P=V²/R – or, in the case of a loudspeaker, we use the term impedance (P=V²/Z) to include the inductive and capacitive aspects of it electroacoustic character. Since a loudspeaker requires an alternating current (regardless of direction, current still heats the coil), the highest continual voltage capable of driving it is half of the peak-to-peak supply. The signal can only increase to the limits of the supply, where clipping occurs (as shown, here).

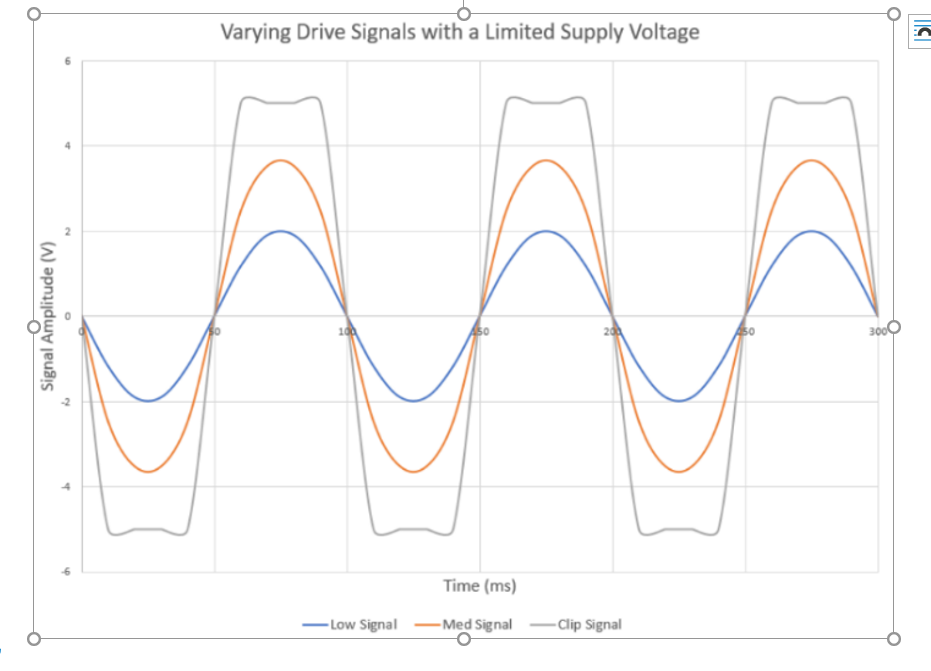
So, let’s say you have a 10V peak-to-peak supply (e.g. ±5V). With sine waves (remember, all audio waves can be analysed as a “sum of sines”), current varies over time. So, we need to consider the average effect of this current. This is where that RMS (the mathematical root mean square) comes in. The RMS value of any sine wave is its peak value divided by  (only consider the magnitude – polarity has no effect, as the “square” in root mean square makes all power positive). Continuing this example, if you have a speaker with a nominal impedance of 8W, the power would pretty much max out at:

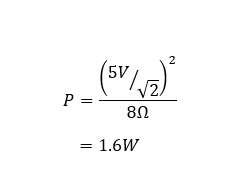
Note that this power is reduced with higher impedances. Since a driver’s nominal impedance is typically the lowest point on its impedance curve, it’s at this point that we consider the power rating. After all, the power rating is a maximum value. Any lower requirement is still acceptable for design purposes. For other supply voltages and/or impedances, just use the appropriate values in the equation above to determine your needs.

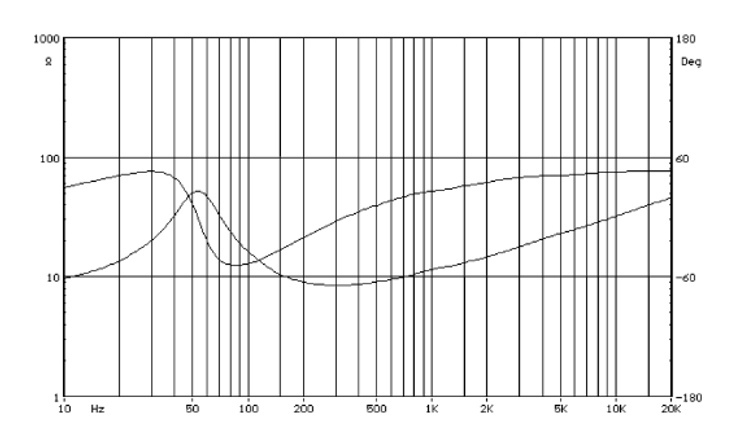
Selecting an average power rating of 2W should suffice for this application. And, although, an absolute worst case of clipping the signal to a square wave would result in a power of a little over 3W, a peak power of 3W should work, as well. If you’re using a square wave as an audio source, you’ve got bigger problems with your design than a power rating…

As always, if you have any questions, our audio engineers are here to provide support. Just contact us and we’re happy to help.